CS229：06-牛顿法

牛顿法（英语：Newton’s method）又称为牛顿-拉弗森方法（英语：Newton-Raphson method），它是一种在实数域和复数域上近似求解方程的方法。方法使用函数$\displaystyle f(x)$的泰勒级数的前面几项来寻找方程$\displaystyle f(y)=0$的根。

——维基百科

牛顿法可以通过迭代逼近的方法，求得函数$f(x)=0$的解。

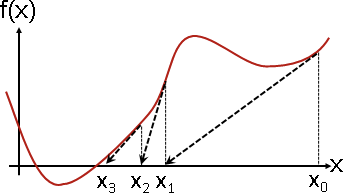
1. 先初始化某个点$x_0$，对该点求导数$f’(x_0)$，可以得到一条切线；
2. 切线会和横轴再有一个交点$x_1$，然后再重复第一步；
3. 直到$f(x_n)=0$

通过一系列推导，我们可以得知：

$$x_{i+1}-x_{i}=\frac{f(x^{(i)})}{f'(x^{(i)})}$$

于是，我们可以将牛顿法用于极大似然估计，也就是求$l(\theta)$的最大值，可以看做是求$l’(\theta)=0$的解。

那么，每次迭代就可以写成：

$$\theta^{(t+1)}=\theta^{(t)}-\frac{l'(\theta^{(t)})}{l''(\theta^{(t)}}$$

更一般地，可以写成：

$$\theta^{(t+1)}=\theta^{(t)}-H^{-1}\nabla_\theta l$$

其中，$H$是$l(\theta)$的 Hessian 矩阵：

$$H_{ij}=\frac{\partial^2l}{\partial\theta_i\partial\theta_j}$$

但这个方法有个缺点，每次迭代的时候，都需要重新计算$H^{-1}$，虽然牛顿法对函数$f$有很多要求和限制，但对于 logistic 函数而言，足够有效。